相関がありそうないくつかのデータから近似関数を求める手法です。40年ほど前、自分の卒論を書いている時に知りました。理解した時はいたく感動しました。世の中には賢い人がいるものです。
当時はWindowsもインターネットなどという物もなかった時代ですから、図書館に入り浸って理解するのに相当時間がかかりました。同じように最小二乗法をはじめて勉強して理解したいという人のために、可能な限り簡単に解説してみます。今では何も考えなくてもエクセルで近似曲線が描けてしまいますが、理解して使うか、理解しないで使うかは雲泥の差になることでしょう。
LSM:Least Square Method
高校や大学で習う数学を、普段社会に出てからも使っている人は少ないと思います。数学の方面に進んだ一部限られた人に限定されるでしょう。三角関数にしても、因数分解にしても、微積にしても、日常的に使う人はほとんどいないと思います。ましてやフーリエ変換だのマクローリン展開だの、大学で習う数学は、今まで実社会で役立ったことはありません。しかし、最小二乗法は別です。唯一、今でもよく使う数学です。もっとも、大学で卒論の手伝いをすることが多いからかもしれませんが、数学とはまったく別の生物系の分野でも頻繁に使うので、おそらくあらゆる分野に応用できる、大変有用な数学だと思います。
1次式の近似
例えば、何かの成長を調べたとします。生まれたハムスターの体重を日を追って計測したデータでもいいし、発芽したもやしの長さでもいいでしょう。日を追うごとに成長して、日数と重さや長さは明らかに関係がありそうです。一般的には日数が増えるとハムスターの体重やもやしの長さは増えます。それを関数で表せないかという試みです。
関数で表せるようになると、未来を予測することができるようになりますし、一つの個体が普通よりも成長が遅いとか早いといった判断をすることもできるようになります。
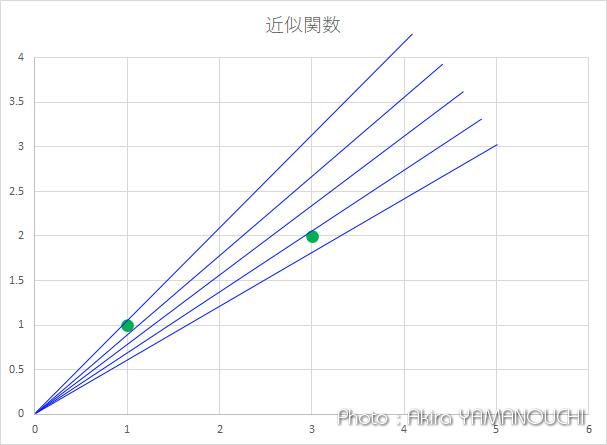
まずはグラフにデータをプロットしてみましょう。そしてじっくり眺めます。何となく直線状に並んでいるようでしたら、1次式でうまく近似できる可能性があります。
単純化するため、原点を通る一次式 y = ax を想定します。この a を求めれば近似直線になり、未来を予測できるようになります。
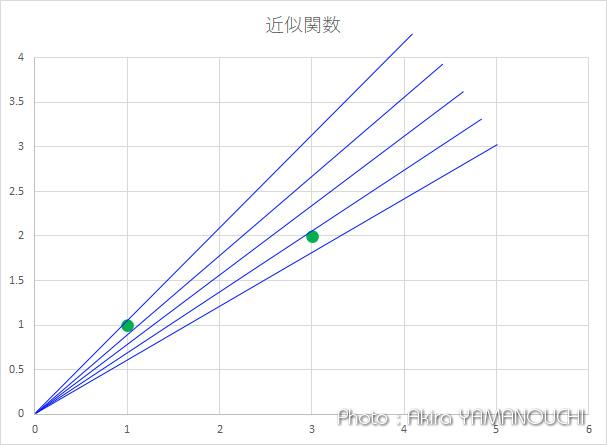
さて、どうすれば最適な a が求まるでしょうか。y=axは原点を通る直線の方程式で、aの値によって角度が変わります。プロットした点群の真ん中辺を通るように決めたいということは分かると思いますが、厳密にはどういうことでしょうか。
一つの考え方として、同じxの値の想定関数とデータのyの値の差、つまり、同じxの値の点と線の距離を求めて、その距離の合計が最も小さくなるような a を求めれば最適な近似直線になるでしょう。
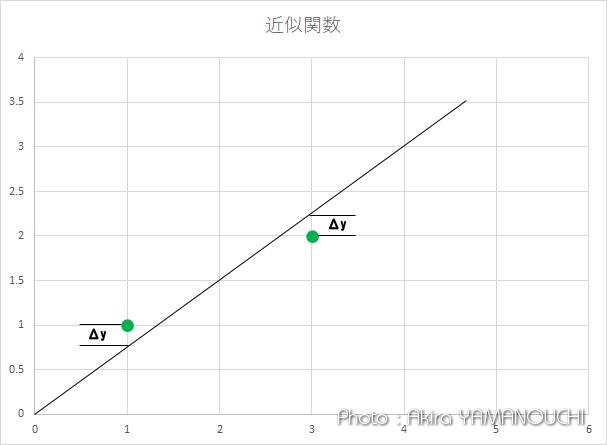
その時のaを求めます。
点と直線との距離の求め方は、直線に垂線を下した距離とかいろいろ考えられますが、単純に同じx座標のyの値の差を考えます。
最小二乗法のミソは、この求めた関数と点のyの差を考えるのではなく、差の二乗を扱うことです。2つの点の中間を通る直線を想定すると、差だけで考えるとプラスとマイナスになってしまうので0になってしまいます。二乗すると必ずプラスになるので、結果が残ります。
それを合計したものを差の指標とします。実はこれ統計学の「分散」と同じ考えなのですね。
また、二乗することによって、差を表す関数がaの2次方程式になります。2次方程式は、放物線ですから、必ず極小値が存在します。それが求める解になります。簡単に言うと、これが最小二乗法の基本的な考え方になります。
簡単なサンプル
簡単な例で計算してみましょう。
| 点 | (x,y) |
| 1 | (1,1) |
| 2 | (3.2) |
次のような2つの点があります。統計学的にはこんな2つの点だけではそれに相関関係があるかどうかも分からないので、近似関数を求めるべきものではありませんが、ここは最小二乗法の考え方の例なので、統計学的な優位性などは無視します。
この2点を近似する直線 y = ax を求めます。
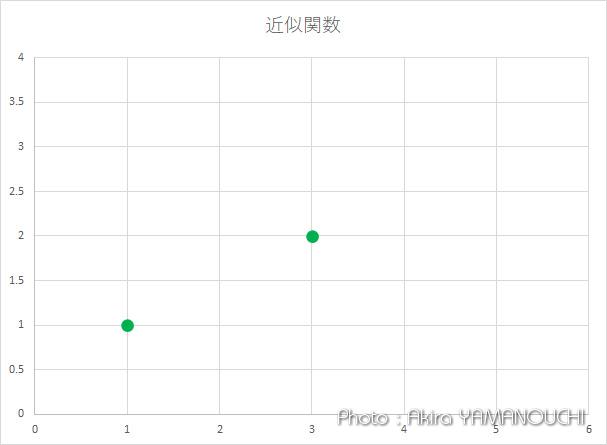
x=1の時の直線上のyの値はaです。したがって、点1とのyとの差は1-aで、その二乗は(1-a)2となります。
x=3の時の直線上のyの値は3aです。点2のyとの差は2-3aで、その二乗は (2-3a)2 となります。
距離の二乗を合計した関数f(a)は、
f(a) = (1-a)2 + (2-3a)2
= 1-2a+a2+4-12a+9a2
= 10a2 -14a+5
直線との距離の二乗和の関数がaの2次式で表せました。これは下に凸の放物線です。その極小値を求めればよいことになります。それは接線の傾きが0となるポイントです。
微分しましょう。
f'(a) = 20a-14
これが0となるaを求めます。
f'(a) = 20a-14 = 0
20a=14
a=14/20=7/10
でaが7/10と求まりました。
したがって近似直線は y = 0.7x となります。実際にグラフを描いてみると確かに最適解になっていることがわかります。高々2つのデータなのでこれだけでは何とも言えませんが、数十、数百のデータで処理をするとより高精度の近似関数が導き出されるでしょう。
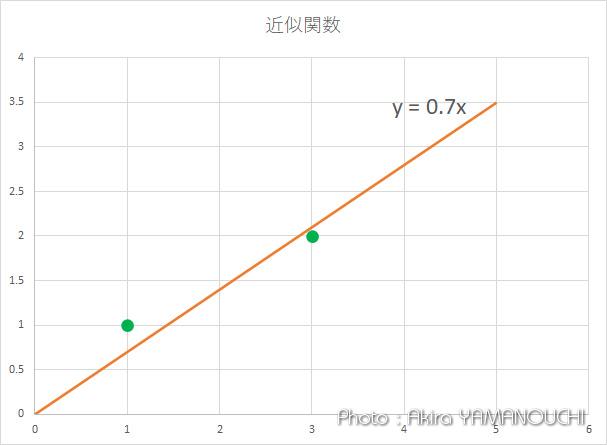
実践
サンプル数が増えると計算が面倒なので、ちょっと工夫してエクセルで計算すると良いでしょう。
n個のデータがあるとき( x1 , y1 ) … ( xn , yn ) を元にf(a)を求める場合、2点の時と同様に考えます。n個のデータなので、一般式にまとめてみましょう。
f(a) = (y1-ax1)2 + (y2-ax2)2 + (y3-ax3)2 + … +(yn-axn)2
= y12-2ax1y1+x12a2 + y22-2ax2y2+x22a2 + y32-2ax3y3+x32a2 + … + yn2-2axnyn+xn2a2
= (x12+x22+x32+…+xn2) a2 – 2(x1y1+x2y2+x3y3+…+xnyn)a + y12+y22+y32+…+yn2
と変形することができます。Σを使うともっとスマートな表記になりますが、Σにアレルギーを持つ人が多いので、あえて使いません。n個のxy座標と近似直線との距離の二乗和を表す一般式ができました。
これを微分すると、
f'(a) = 2(x12+x22+x32+ … +xn2)a – 2(x1y1+x2y2+x3y3+ … +xnyn)
となり、傾き0の時が極小値なので、
a = (x1y1+x2y2+x3y3+…+xnyn) / ( x12+x22 + x32 +…+ xn2 )
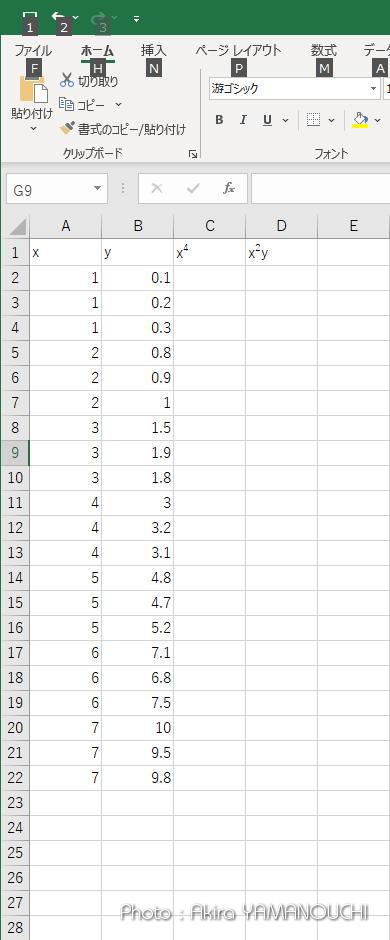
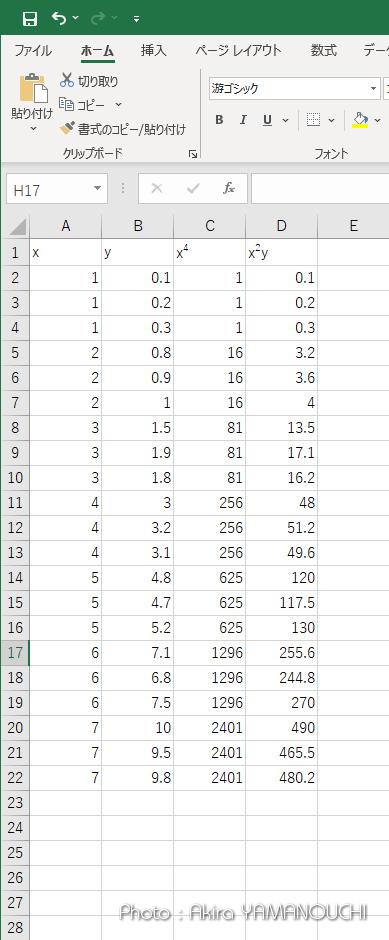
となります。これはエクセルで簡単に計算できますね。x、y、の他に、xy、x2 の列を作ってオートフィルで計算させて合計を求めれば良いのです。
手計算させられたらうんざりしますが、エクセルなら簡単 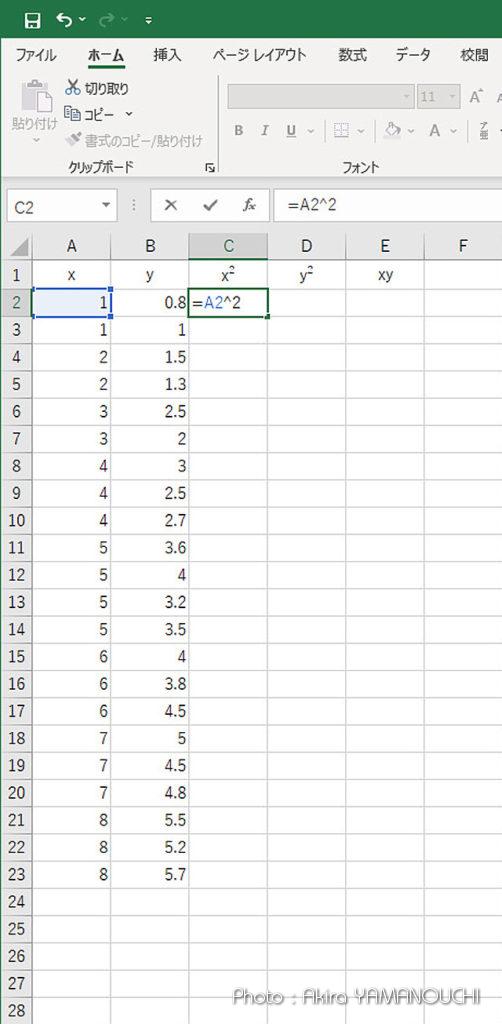
一つだけ関数を定義して、後はオートフィル
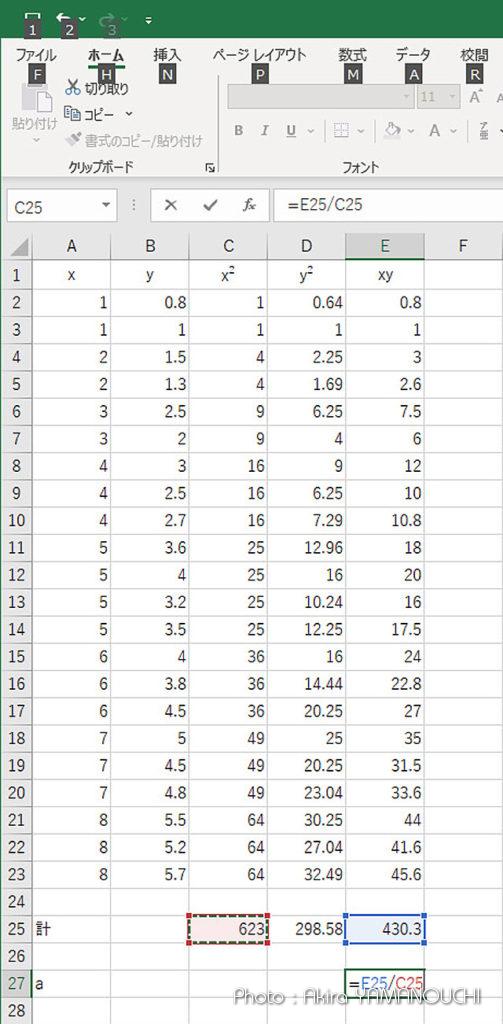
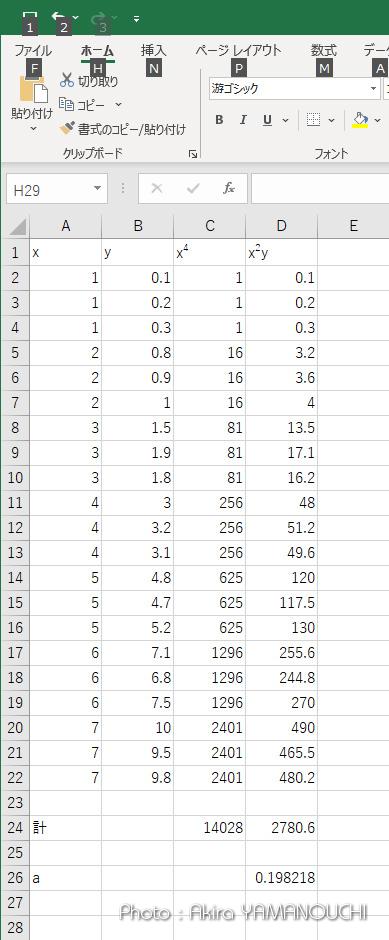
縦に全部足すのも一発です 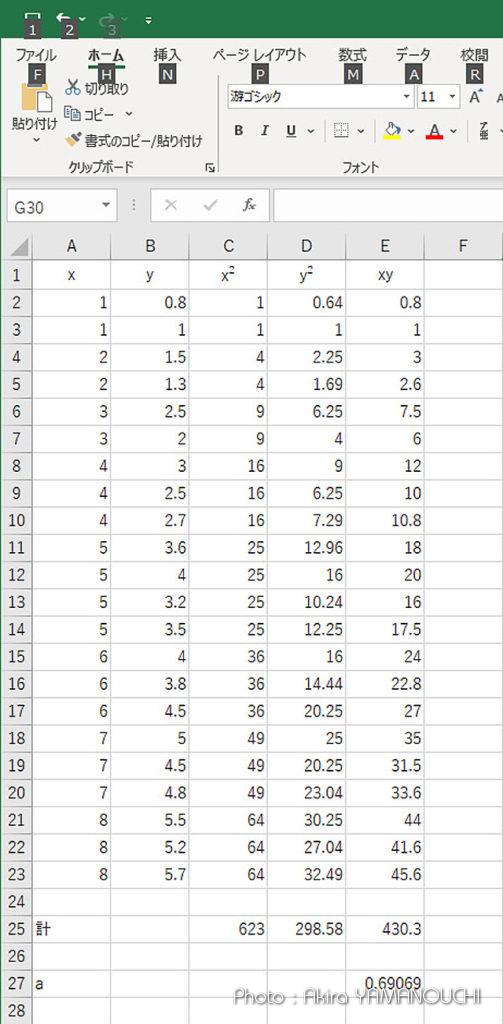
このくらいであれば数分でできてしまいます
aの値は0.69069となりました。近似直線関数は、y = 0.69069x となります。
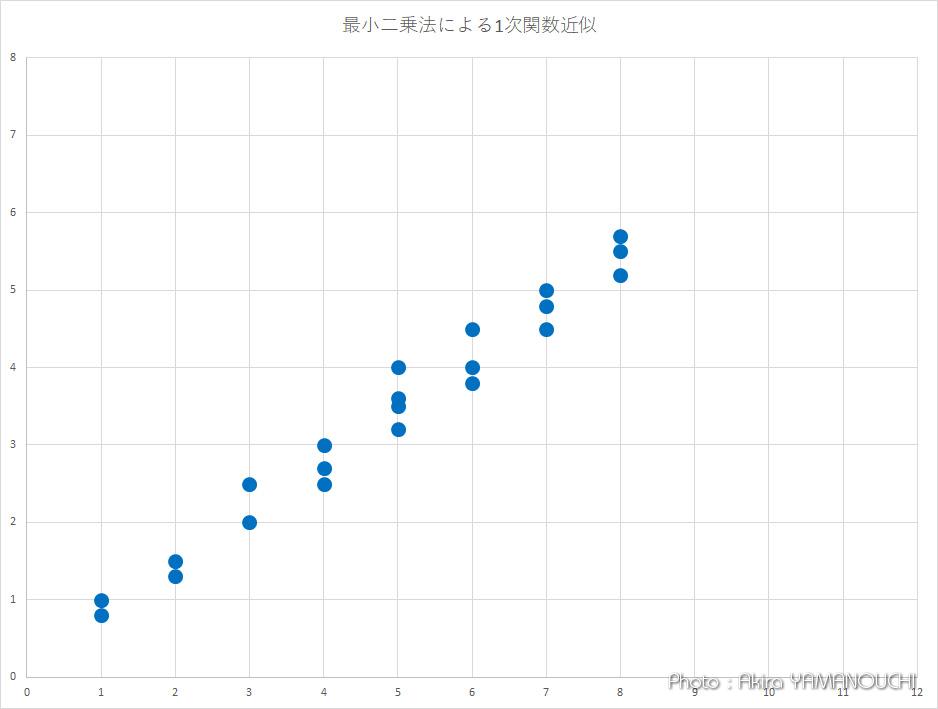
y = 0.69069x のグラフを重ねてみましょう。
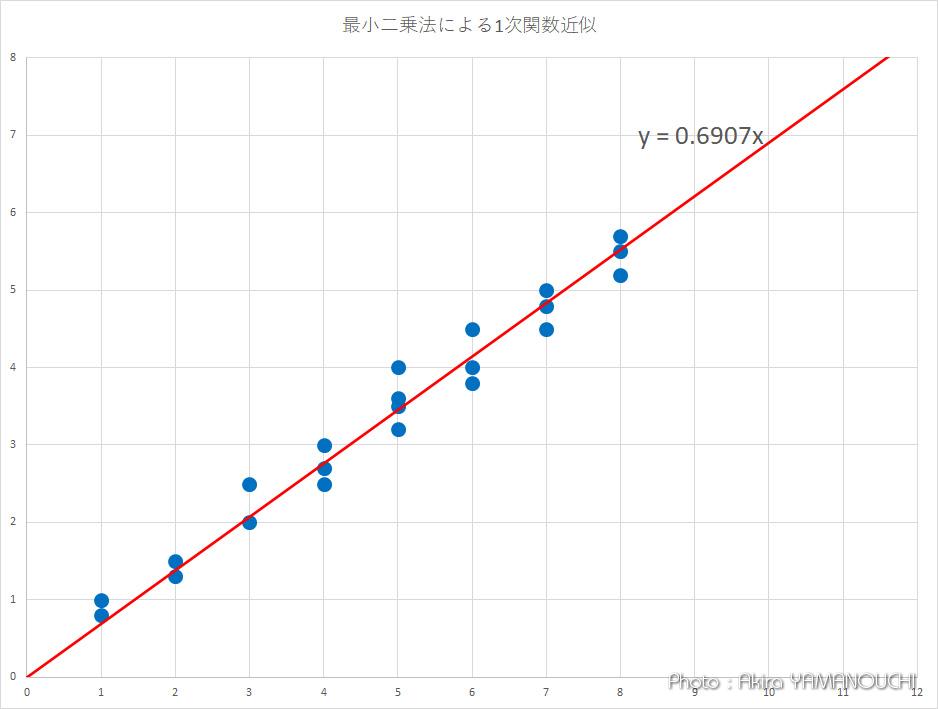
かなりそれらしくフィットしていることがわかります。
「何だかよくわからないけどできた」のではなく、「最小二乗法を完全に理解して近似関数を求める」のではここからの応用に違いが出てくるでしょう。
2次式の近似
実験結果をプロットしてみると、どうも直線的な分布ではなく、2次関数的に増加する傾向が見れれることがあります。例えば、時間の経過とともに粘菌が広がる面積とか、山火事が広がる面積とか、面積に関わることは、理屈の上からも2次関数的に分布する傾向があります。
その場合も考え方は同じです。1次式の近似が理解できていれば、臆することはまったくありません。
想定する近似関数が、y = ax2 になるだけです。
n個のデータの時の差分二乗和の一般式は、
f(a) = (y1-ax12)2 + (y2-ax22)2 + (y3-ax32)2 + … +(yn-axn2)2
= y12-2ax12y1+x14a2 + y22-2ax22y2+x24a2 + y32-2ax32y3+x34a2 + … + yn2-2axn2yn+xn4a2
= (x14+x24+x34+…+xn4)a2 – 2(x12y1+x22y2+x32y3+…+xn2yn)a + y12+y22+y32+…+yn2
と、これもきれいなaの2次式になるので、同様に微分すると、
f'(a) = 2 (x14+x24+x34+…+xn4)a – 2(x12y1+x22y2+x32y3+…+xn2yn) = 0
a = (x12y1+x22y2+x32y3+…+xn2yn) / (x14+x24+x34+…+xn4)
次数が増えていますが、エクセルで計算すればお茶の子さいさいです。
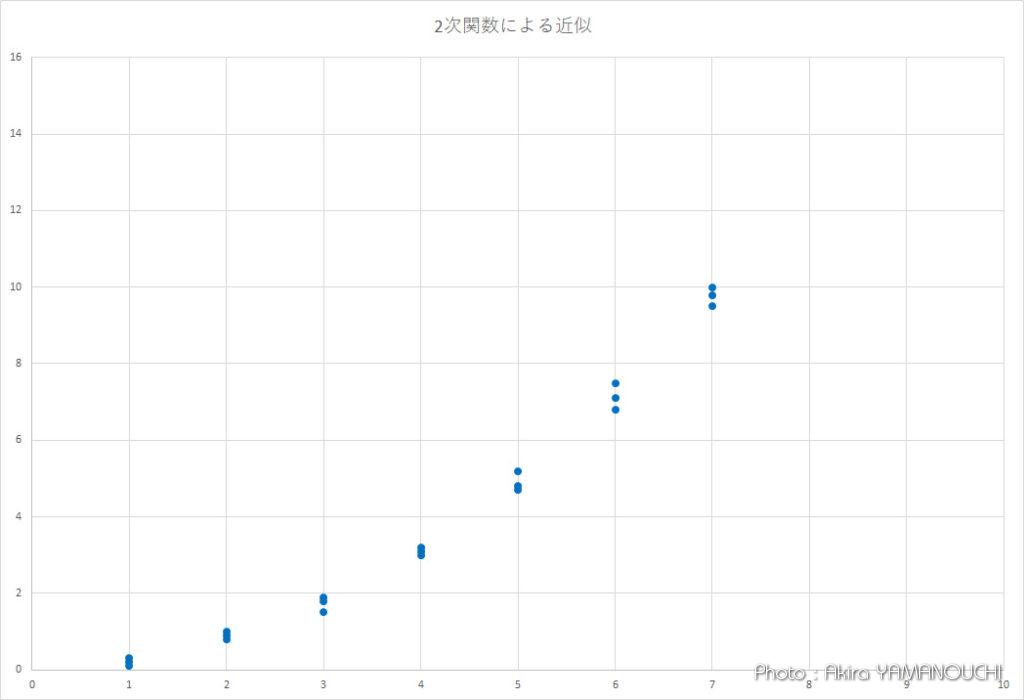
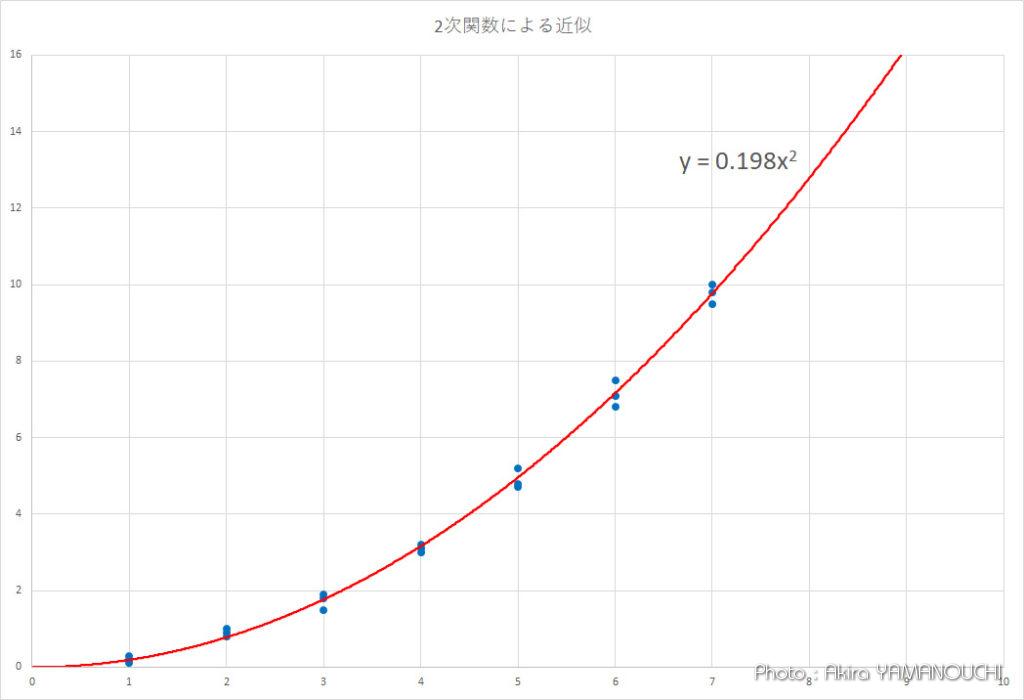
3次式の近似
ここまで来るともう大丈夫だと思います。3次式だろうと、4次式だろうと、次数が増えても大したことはありません。しかし、多くの場合、使用するのは3次式くらいまででしょう。3次式は体積や体重など、3次元的なものを扱う時にはよく使用します。
想定する近似関数が
y = ax3
になるだけですから、差の二乗和を求める関数は、
f(a) = (y1-ax13)2 + (y2-ax23)2 + (y3-ax33)2 + … +(yn-axn3)2
= y12-2ax132y1+x16a2 + y22-2ax23y2+x26a2 + y32-2ax33y3+x36a2 + … + yn2-2axn3yn+xn6a2
= (x16+x26+x36+…+xn6)a2 – 2(x13y1+x23y2+x33y3+…+xn3yn)a + y12+y22+y32+…+yn2
となります。同じく微分すると、
f'(a) = 2 (x16+x26+x36+…+xn6)a – 2(x13y1+x23y2+x33y3+…+xn3yn) = 0
a = (x13y1+x23y2+x33y3+…+xn3yn) / (x16+x26+x36+…+xn6)
次数が増えていますが、単なる定数なのでエクセルで計算すればお茶の子さいさいです。
サンプル
イグアナのSVL(頭胴長)と体重の関係。
イグアナなどの爬虫類は基本的に体形(プロポーション)はあまりかわらず、ほぼ相似形に成長するため、体積は3乗に比例します。近似曲線は理屈の上からも3次関数が適しています。y = ax3 と想定して最小二乗法でaを求めます。
ただし、さすがのエクセルも途中で6乗の処理が出てくると、大きな数だとすぐにオーバーフローしてしまいます。適宜データをすべて6乗してもオーバーフローしない値に処理しておきます。SVLはmmのデータだったのですが、数百という値を6乗すると計算できなかったので、すべて1/100にして計算しました。
3次関数 y = ax3できれいにフィッティングしていることが分かります。
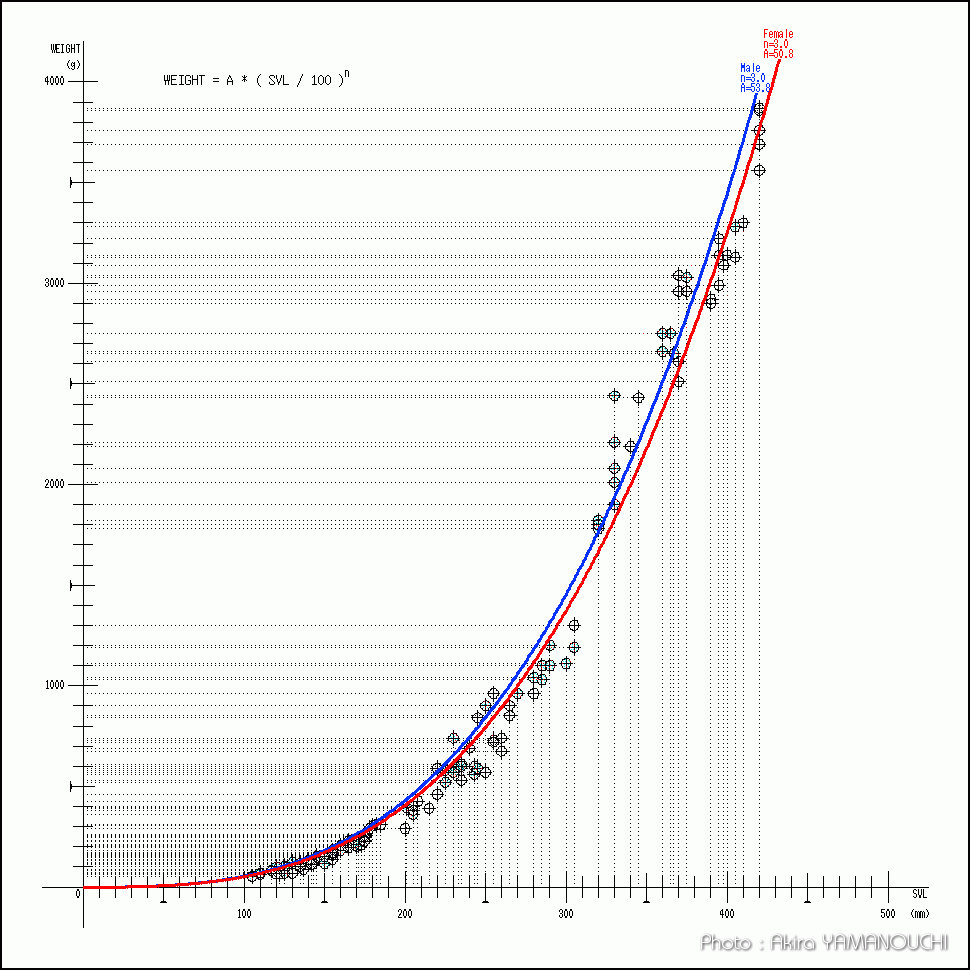
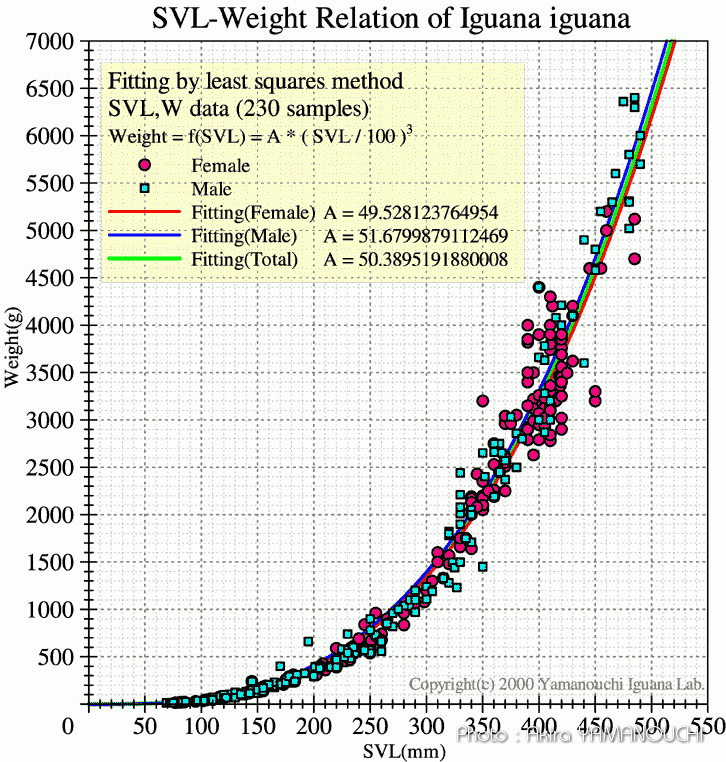
適度なデータが集まると近似曲線より上のデータは太り過ぎ、下のデータは痩せすぎの指標になります。測定データがない範囲の予測をすることもできるようになります。また、雌雄で別々に処理することにより、オスとメスの関数を導き出せます。それにより、雌雄判別に使える可能性もあります。
以上のように、最小二乗法は様々な分野で相関関係があるデータを処理する上で有用な武器になります。大学で習う数学で一番実用的な計算ではないでしょうか。今ではエクセルで簡単に近似曲線は描けますが、何をしているのか知らずに使うわけにはいきません。学生の頃は頭も柔らかいはずなので、考え方だけでも理解して使ってください。そこから様々な応用が広がってくると思います。